lunes, 24 de marzo de 2014
Teoremas del seno y
del coseno
Introducción:
·
Trigonometría
Rama de las matemáticas que estudia las
relaciones entre los lados y los ángulos de los triángulos; etimológicamente
significa `medida de
triángulos'.
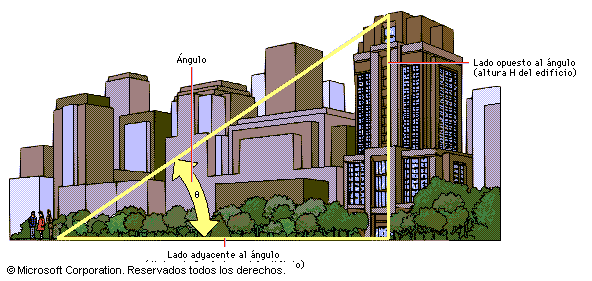
Las primeras aplicaciones de la trigonometría se hicieron en los campos de la navegación, la cartografía y la astronomía, en los que el principal problema era determinar una distancia inaccesible, es decir, una distancia que no podía ser medida de forma directa, como la distancia entre la Tierra y la Luna. Se encuentran notables aplicaciones de las funciones trigonométricas en la física y en casi todas las ramas de la ingeniería, sobre todo en el estudio de fenómenos periódicos, como el flujo de corriente alterna.
Las primeras aplicaciones de la trigonometría se hicieron en los campos de la navegación, la cartografía y la astronomía, en los que el principal problema era determinar una distancia inaccesible, es decir, una distancia que no podía ser medida de forma directa, como la distancia entre la Tierra y la Luna. Se encuentran notables aplicaciones de las funciones trigonométricas en la física y en casi todas las ramas de la ingeniería, sobre todo en el estudio de fenómenos periódicos, como el flujo de corriente alterna.
Las dos ramas fundamentales de la trigonometría
son la trigonometría plana y la trigonometría esférica…
Trigonometría plana:
Se ocupa fundamentalmente de la
resolución de triángulos planos. Para ello, se definen las razones
trigonométricas de los ángulos y se estudian las relaciones entre ellas.
Trigonometría
esférica:
La trigonometría esférica, que se usa
sobre todo en navegación y astronomía, estudia triángulos esféricos, es decir,
figuras formadas por arcos de circunferencias máximas contenidos en la
superficie de una esfera. El triángulo esférico, al igual que el triángulo
plano, tiene seis elementos: los tres lados a, b, c, y los
tres ángulos A, B y C. Sin embargo, los lados
de un triángulo esférico son magnitudes angulares en vez de lineales, y dado
que son arcos de circunferencias máximas de una esfera, su medida viene dada
por el ángulo central correspondiente. Un triángulo esférico queda definido
dando tres elementos cualesquiera de los seis, pues, al igual que en la
geometría plana, hay fórmulas que relacionan las distintas partes de un
triángulo, que se pueden utilizar para calcular los elementos desconocidos.
·
·
Triángulos oblicuángulos
Se contrapone a rectángulo, en
sentido estricto. Pero cuando se habla de triángulos oblicuángulos no se
pretende excluir al triángulo rectángulo en el estudio, que queda asumido como
caso particular. No obstante cuando el triángulo es rectángulo, porque se dice
expresamente que lo es, el problema se reduce, tiene un tratamiento particular
y no se aplican las técnicas generales de resolución que vamos a ver
seguidamente.
Los elementos de un triángulo oblicuángulo son los tres ángulos A, B y C y los tres lados respectivos, opuestos a los anteriores, a, b y c.

Sistema Centesimal
En este sistema la circunferencia se considera dividida en 400 grados, cada grado en 100 minutos y cada minuto en 100 segundos. A estos grados se les llama grados centesimales. Las abreviaturas son: grados centesimal (g.c.); minuto centesimal (m.c.), y segundo centesimal (s.c.). Así,
| Un grado centesimal es la medida del ángulo central de un círculo, de amplitud igual a la 400 ava parte del mismo. |
Sistema Sexagesimal
Este sistema de medir ángulos es el que has empleado durante tus primeros estudios; en él, la circunferencia se ha dividido en 360 partes iguales llamadas grados. Un grado sexagesimal se denota 1°. Esto significa que un ángulo recto tiene 90° y que el ángulo completo cuyo arco es toda la circunferencia tiene 360°.
| Un grado sexagesimal es la medida del ángulo central de un círculo, de amplitud igual a la 360 ava parte del mismo. |
Si queremos medir ángulos que no corresponden exactamente a un número entero de grados, entonces de divide cada grado en sesenta partes, llamadas minutos. Un minuto se denota 1' y es la sesentava parte de un grado. Cada minuto a su vez, se divide en sesenta partes llamadas segundos. Un segundo se denota 1'' y es la sesentava parte de un minuto.
Por ejemplo, en unidades sexagesimales, los ángulos se expresan como en los siguientes ejemplos:
α = 30° 28' 49''
β = 17° 9' 30''
γ = 0° 23'
Sistema Cíclico
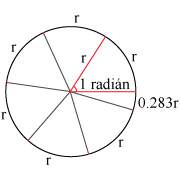
Este sistema se forma y define de la manera siguiente: en una circunferencia cualquiera se señala un arco de longitud igual al radio de la circunferencia y se trazan los radios correspondientes a cada extremo del arco; el àngulo central que forman estos dos radios se llama radián; el radián se divide decimalmente, es decir, en décimos, centésimos, milésimos, etc. Así,
| El radian es el ángulo central subtendido por un arco igual a la longitud del radio del círculo |
Conversión de medidas de ángulos
Un radián se define como la medida de un ángulo central cuyos lados cortan un arco de igual longitud al radio del círculo. Ya que la longitud de este arco es igual a un radio del círculo, se dice que la medida de este ángulo es un radián y equivale a 57.296º.
Suscribirse a:
Entradas (Atom)